位、字节和进制¶

计算机使用位（bit）来表示二值信号，单个位通常不是非常有用。

把多个位组合在一起，对位模式赋予不同的含义，我们就能够表示任何有限集合的元素。例如，计算机使用 8 个位组成的字节（byte）作为最小可寻址的内存单位，而不是单个位。

通过组合位，我们可以表示更多的数值。虽然计算机本质上依然在处理位，但是我们可以创造性地抽象出多种不同的数据表示：

文本
图片
音频
视频
……

我们需要一些方法来表示基本数据类型，本章将优先介绍计算机的数学进制。

二进制 Binary¶

日常生活中，我们使用十进制数字系统，可能的原因是我们有十个手指，但是十进制与其他数字系统相比并没有什么不同。

计算机由于硬件的特性，经过历史的选择，最终保留了二进制数字系统。二进制数字系统是我们能够得到的最简单的数字系统——只有两个数字 0 和 1。

位（bit）是由英文 “binary digit” 简写而来，用于表示一个二进制数字位。这是组成信息块的最基本单位。位的概念可以理解为 1 或 0、开或关、是或否、真或假的值。

下图分别展示了十进制和二进制数字系统的计算原理。

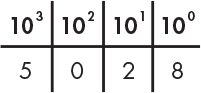
base-10

\[5028 = 5 * 10^3 + 0 * 10^2 + 2 * 10^1 + 8 * 10^0\]

base-2

\[5028 = 1 * 2^{12} + 1 * 2^9 + 1 * 2^8 + 1 * 2^7 + 1 * 2^5 + 1 * 2^2\]

字节（byte）是由 8 个位组成。由于计算机内存是一个由地址编号的大号字节数组，通过地址可以访问每一个字节，所以在计算机编程中，我们无法直接访问某个位。字节是我们能够处理的最小单位。

根据上述计算原理，我们可以得出一个字节可以表示的数字范围是 \([0, 255]\)。

小技巧：基于基数（Base）的乘法和除法

乘法需要向右移动 1 位并补零：1450 * 10 = 14500 对比 1100 * 2 = 11000
除法只需要向左移动 1 位：1450 / 10 = 145 对比 1100 / 2 = 110

开心一刻

基于多项式展开原理设计的小游戏：Guess Number

十六进制 Hexadecimal¶

十六进制（hexadecimal）是使用 16 个不同的符号表示的数字系统，“0”-“9”表示值 0 到 9，“A”-“F”（或小写）表示 10 到 15 之间的值。

由于二进制数字阅读比较困难，在软件开发中，我们一般使用十六进制数字系统，因为它们提供了更人性化的表示。每个十六进制数字代表四个位，也称为半字节（nibble）。例如，一个字节的值范围从 00000000 到 11111111 的二进制形式，可以方便地表示为十六进制的 00 到 FF。

为了便于区分，在 C 语言中二进制使用 0b 前缀，十六进制使用 0x 前缀。例如，0xf5 可以表示为 0b11110101。

由于十六进制和二进制的对应关系，两者之间很容易进行转换，本课程要求大家能够通过记忆一些规律进行快速转换。

base

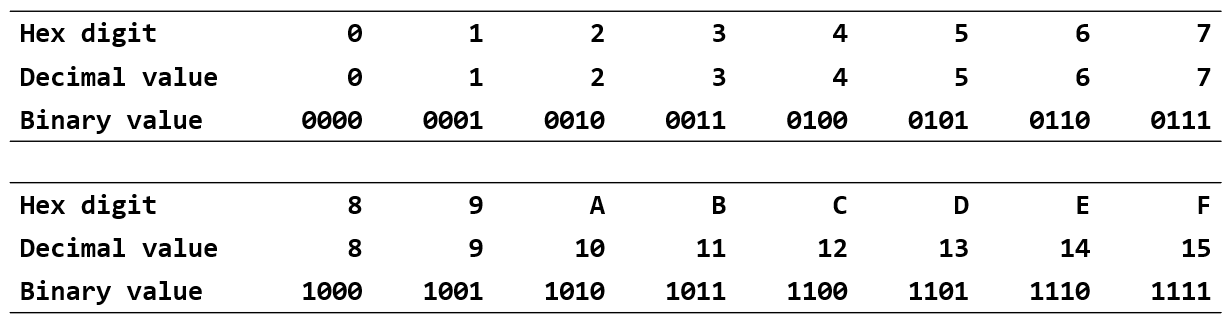
不同进制的比较¶

一张表比较下三种进制之间的优劣：

进制	表示形式	优点	缺点
十进制	`165`	可读性强	不好对应到比特位
二进制	`0b10100101`	清晰地表示计算机位模式	可读性差
十六进制	`0xa5`	既便于转换到二进制位模式，又便于书写和阅读