位运算及其应用¶
到目前为止,我们已经知道数据在计算机内部是以二进制形式存储的。那么,我们如何操作二进制形式的数据呢?
布尔位运算¶
在 C 语言中,一个很有用的特性是可以按位进行布尔运算,对应的操作符是:|(OR),&(AND),~(NOT),^(XOR)。
OR 的任意一个操作数为真(1),结果就为真(1);AND 的任意一个操作数为假(0),结果就为假(0);XOR 的两个操作数不同时,结果为真(1)
output = a | b; output = a & b; output = a ^ b;
NOT 的操作数为真(1)时,结果就为假(0);反之,操作数为假(0)时,结果就为真(1)
output = ~a;
辨析:逻辑运算
在 C 语言中,逻辑运算(||,&&,!)很容易和位运算混淆。逻辑运算认为非 0 为 true,0 为 false。
逻辑运算是按整体数值来计算结果的,并不是在位级别上进行操作;这是区别于位运算最大的地方。
移位运算¶
移位运算也可以称为一种位运算,因为该操作符将值当作一系列的位来对待,而不是一个整体数值。但由于寄存器的位数固定,所以在移位过程中,总会有一些位被移出(shifted out)寄存器,也会有一些位被移进(shifted in)寄存器。
x << k; // 该表达式等于将 x 向左移动 k 个位后的值(x 不变)
x >>= k; // 将 x 向右移动 k 个位(x 改变)
补充:k 的范围
如果 x 是一个 int 整型,则 x 将由 32 个位组成。如果执行下面的操作:
x << 32;x >> 36;x << 40;
参考书介绍说,这样的情况会先计算 k 和位数的模,再按模量来移动,上述语句最终移动的位数将变为 0、4 和 8 位。
在 C 语言中,k 为负值或大于等于数据类型宽度是未定义行为(Undefined Behavior),上述语句并不会真正工作。
左移操作¶
左移操作将二进制位模式向左移动指定数量的位置。移动之后,低位(lower order)增加的部分用 0 补充,高位多余的部分将会丢失。
00110111 << 2 // 11011100
01100011 << 4 // 00110000
10010101 << 4 // 01010000
右移操作¶
右移操作将二进制位模式向右移动指定数量的位置。移动之后,低位多余的部分将会丢失,但是高位(higher order)并不会默认补充 0。
对于无符号整型,高位补充 0,这种右移操作称为逻辑右移(Logical Right Shift)
unsigned short ux = 16; unsigned short uy = x >> 4; // 0000 0000 0001 0000 -> 0000 0000 0000 0001
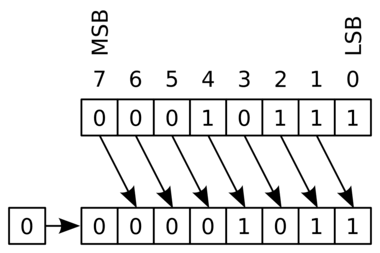
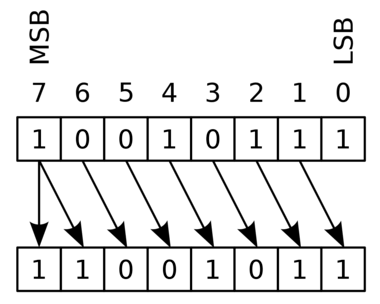
对于有符号整型,高位补充符号位,这种右移操作称为算术右移(Arithmetic Right Shift)。
虽然 C 标准并没有规定有符号整型必须采用算术右移,但是大部分编译器都默认这个行为,所以我们可以把这个行为当作事实来对待。
short x = 16; short y = x >> 4; // 0000 0000 0001 0000 -> 0000 0000 0000 0001 x = -16; y = x >> 4; // 1111 1111 1111 0000 -> 1111 1111 1111 1111
陷阱:注意操作符的优先级
由于加法操作符优先级比移位运算符高,所以表达式 1<<2 + 3<<4 在 C 语言中的解释是 1 << (2+3) << 4。
为了避免不必要的麻烦,尽量多加一些括号,比如这样 (1<<2) + (3<<4)。
位掩码¶
位操作在嵌入式等涉及到硬件操作的领域应用较为广泛,其中一个应用场景是对一组位模式进行选择性操作,即屏蔽掉部分位,只对感兴趣的部分进行修改,这种操作称为位掩码(Bitmask)。
位运算在底层库、嵌入式、网络、图形学领域有大量应用,即使不深入底层,掌握这些常见操作也是非常有必要的。
将指定的位设置为 1¶
置 1 操作,即打开某些位,可以使用按位或运算 | 。
Y | 1 = 1:按位或运算|搭配 1 可以将位设置为 1Y | 0 = Y:按位或运算|搭配 0 可以保持位状态不变
示例:在较高的半字节(位 4、5、6、7)上置 1,同时保持较低的半字节(位 0、1、2、3)不变。
10010101 10100101
| 11110000 00010000
-------- --------
11110101 10110101
以上示例也可以理解为,求两组位模式的并集。
将指定的位设置为 0¶
在实践中,更常见的是置 0 操作,可以使用按位与运算 &。
Y & 1 = Y:按位与运算&搭配 0 可以将位设置为 0Y & 0 = 0:按位与运算&搭配 1 可以保持位状态不变
示例:在较高的半字节(位 4、5、6、7)上置 0,同时保持较低的半字节(位 0、1、2、3)不变。
10010101 10100101
& 00001111 11001111
-------- --------
00000101 10000101
以上示例也可以理解为,求两组位模式的交集。
查询某个位的状态¶
按位与运算 & 稍作变化就可以进行查询操作。结果为 true,则查询的位是 1;结果为 false,则查询的位为 0。
示例:查询第 4 个位的状态
10011101 10010101
& 00001000 00001000
-------- --------
00001000 00000000
切换位的状态¶
上述应用,要么同时打开某些位,要么同时关闭某些位,但有些情况下,我们需要关闭一部分位的同时打开另一部分。
按位异或位操作 ^ 可以实现精准的控制。当且仅当 1 的数量为单数时,异或的结果为 1,所以对于 Y XOR 1
当
Y = 1时,1 的数量不为单数,1 XOR 1结果为 0当
Y = 0时,1 的数量为单数,0 XOR 1结果为 1
示例:将第一组较低的半字节(位 0、1、2、3)切换状态,较高的半字节(位 4、5、6、7)保持不变;将第二组所有位切换状态
10011101 10010101
^ 00001111 11111111
-------- --------
10010010 01101010
对于第二组,如果目的是切换所有位模式,也可以使用按位取反位操作 ~。
~ 10010101
--------
01101010